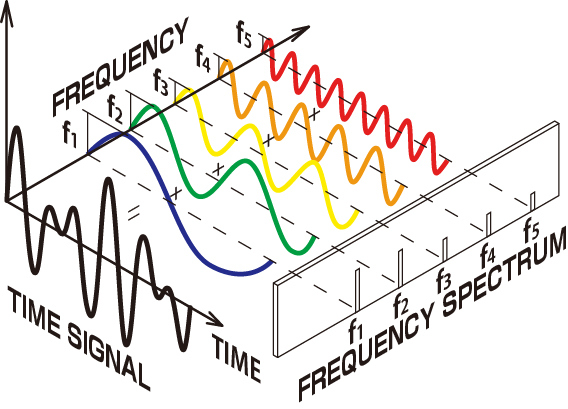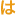

高速フーリエ変換。計算機上で離散フーリエ変換(DFT)を行う際、複素演算時間を大幅に低減させる処理法(アルゴリズム)。DFTのルーチンをいくつかのサブルーチンに分けて計算することで、複素数の乗算回数が減る。
高速フーリエ変換を行う機械。FFT演算専用のハードウェアを持ち、A/D変換器から各種演算機能、表示部、メモリ、記録用プロッタ出力等を備え、ほぼリアルタイムで周波数解析が行える機器。FFT専用機としてオールインワンで操作を行うことができ、高速で演算を行えるメリットがある。
測定機能は、「パワースペクトル」、「自己相関関数」、「クロススペクトル」、「相互相関関数」ができる。また、「伝達関数(周波数応答関数)」、「確立密度関数」、「ケプトラム(対数パワースペクトル)」、「ヒルヘルド変換」の測定など測定機能が豊富。実際には、スピーカの周波数特性、サーボ解析、エンジンなどの回転次数分析、回転トラッキング分析など振動解析に使われる。
国際標準化団体。電気分野を除くあらゆる分野において、標準規格の策定を目的とする民間の非営利の国際機関。日本産業規格(JIS)の調査・審議を行っている日本産業標準調査会(JISC)も加盟しており、JIS規格と関連がある。有名なISO規格としてはカメラのフィルム感度や、品質保証関連のISO9000ファミリーがあるが、電気以外の輸送試験、信頼性試験の試験規格が定められ、振動試験や環境試験の方法、条件など詳細に定めている。
システムが故障するまでの平均時間。平均故障寿命とも言う。平均10年で壊れるシステムであれば、MTTFは10年である。ここで言う故障は修理不可能な意味を含む。修理すれば再度利用できるシステムに対してはMTBF(Mean Time Between Failure)を用いる。
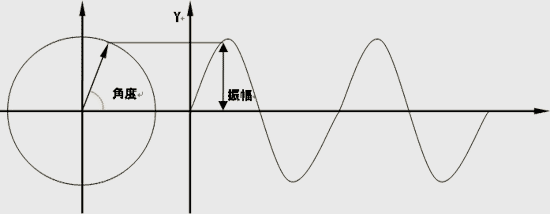
波の方程式の三角関数(正弦波の式)の角度を示す。正弦波の進み角。波動などの波形や周期的な変動における山や谷といった点の位置・状態をひとつの周期の中に特徴付ける量。周期関数の引数。物理的な絶対量を意味するものではないが、時間や角度などで表現する。
また、同じ波の山の位置の違いを位相(角度)であらわすことができる。
単位時間当たりの速度の変化量(割合)。速度の微分量。
1m/s2であれば、1秒間に1m/s変化したことを表す。
加速度aは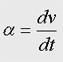 と、表される(v:速度)。
と、表される(v:速度)。
よく使われる加速度として、地球の引力である重力加速度9.80665m/s2(1G)や回転運動の角加速度がrad/s2ある。
また、ニュートンの運動の第二法則「F=m・α」に関係した量である。
振動や衝撃などの加速度を計測する接触型のセンサ。振動センサは圧電効果を利用した圧電式加速度ピックアップが最も普及しており、計測可能な振動数がDC~数100Hz、数Hz~数10kHzと広く高感度なのが特徴で、実在する振動現象をほぼ測定できる。構造的にも機械強度が強く、ダイナミックレンジが広い。また、電荷応答型のため静的感度を持たないので、積分器を使った速度、変位の計測もゼロシフトの誤差を考慮しなくてよい。圧電効果を利用しているので、外部電源が不要な上、取り付けなど取り扱いが簡単。
主に振動発生機に取り付けられ、振動制御および、「加速度」、「速度」、「変位」の振動計測を行い、振動試験装置を構成する重要なセンサ。

マス・バネ・ダンパー系に代表される構造体の機械的「動きにくさ」を表す。
機械インピーダンスが小さければ動きやすく、機械インピーダンスが大きければ動きにくい。粘性、慣性などの機械特性を機械インピーダンス特性で表すことができる。
加えられている力と速度の複素比。
共振は、ある振動系に外部から振動エネルギーを加えると、固有振動を起こすことである。特に、外部からの刺激が固有振動数に近い状態を表す。
共振の特性を表す無次元量としてQ値(quality factor)が用いられる。値が大きいほどエネルギーの分散が小さく、狭い振動数の帯域で共振する。
共振現象には、マス・バネ・ダンパー系に代表する機械、構造物の機械工学的共振、抵抗・インダクタンス・キャパシタ系電気の共振回路に見られる電気工学的共振がある。
機械、構造体の共振現象では次のようなことが問題とされる。
●小さな外力でも大きな振動を起こす現象である。
●構造物の破壊や騒音の増大をもたらす。
機械、構造体の設計や実際の使用環境ではこの共振問題を解決するため、多くは振動試験を実施する。また、共振現象は系の周波数応答のピークを示す現象として捉えられる。
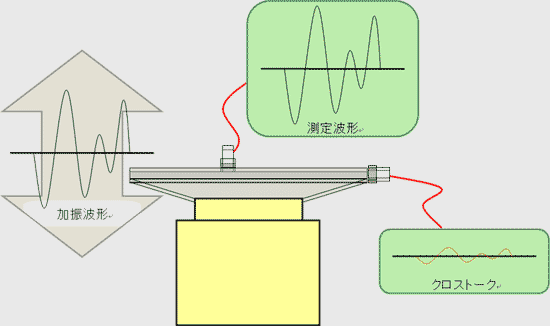
振動試験装置においては、加振軸以外に生じる振動を呼ぶ。
回路中の交流起電力が二つ以上あり、その位相が全て同じである単相交流と、電圧と周波数が同じで、位相が互いに120度ずれている三つの交流を一組にした三相交流がある。
三相交流による送電は、単相交流と比べ、電線一本あたりの送電電力が大きい、同じ送電電力ならば電線の質量を低減できるなどのメリットがある。
システムや物の、ある時点での単位時間当たりの故障発生率。1-稼働率で求められる。
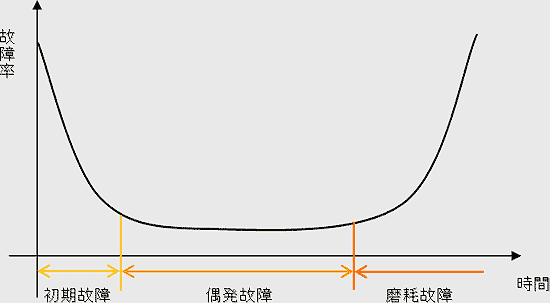
下図は故障率曲線と言い、システムの使用時間と、故障率の関係を表したものである。
形がバスタブに似ていることから、バスタブ曲線とも呼ばれる。
システムを長く使い続けるには、磨耗故障期に入ることを遅らせる、磨耗故障期での故障率を小さくするなど、長寿命化することが重要。
おおむね正弦関数として観測可能な周期的変化を示す波動のことである。
基本的な正弦波はおおよそ次のような関数として記述することができる。
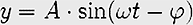
ここで時刻 t を変数、振幅(これは波の中心からの偏差)は A 。また、ω は角周波数、t = 0 における位相である -φ は初期位相という。
数学や信号処理、機械工学、電気工学をはじめ多くの分野で現れる。
1822年フランス人数学者のジョゼフ・フーリエにより、「あらゆる波系の関数は、三角関数の和で記述できる」ことが証明され、今日の振動解析に使用されている。
サイン振動は、振動試験の基本となる振動モードで、ある振動数を固定した周波数応答特性試験や、振動数を掃引(変化)させる共振特性試験など、その他多くの振動特性試験が行える。
交流の実効値は、その交流とおなじ熱効果を発揮する直流の大きさを表す。
交流の瞬間値の2乗平均値の平方根。交流電圧(または電流)の値は常に変化しているので、その大きさを表すのに用いられる。下の式から求められる。
ここで、データ:x[i]、実効値:xrmsと置いている。
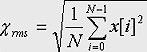
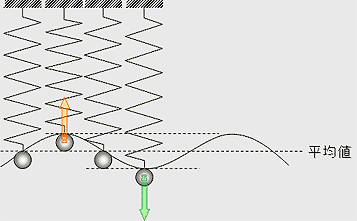
質量mの物体がバネ定数kのバネを介して壁に支持されている、系の外力が作用しないときの振動を自由振動という。この系の振動は振幅、周期、位相、固有振動数の値を持つ。質量mを持つ物体が、バネ定数kのバネと減衰係数cのダッシュ・ポッドを介して支持されている系を、減衰自由振動と呼ぶ。
これにら対し、外力の影響から強制的に引き起こされる振動を、強制振動と呼ぶ。
位置、速度、加速度、温度など、急激な変化のこと。
実際には、自動車が衝突した場合や、冷水を散布した熱衝撃などが該当する。
工業製品の品質検証では多くの耐衝撃試験が行われている。
主に、工業製品の破損を防ぐため、輸送を想定した耐衝撃試験や、自動車のエアバックに使われる衝突センサの動作確認などが有名。
衝撃試験では衝撃加速度別に分類され、一般的なハーフサイン波をはじめ、ハーバーサイン波、のこぎり波、台形波、三角波などがある。試験条件もISO規格、IEC規格、ASTM規格、JIS規格、MIL規格など様々用意されている。
ある量の大きさが、平均より大きくなったり小さくなったり変動する様子。
状態が一意に定まらない事象をいい、周期的な挙動を繰り返す状態を指すことが多い。
簡単に言えば揺れ動くこと。ばね-質量系の単振動に代表される物理的な振動をはじめ、音も空気の振動であり、地震も振動に含まれる。
以下は最もシンプルな振動モデルである、ばね-質量系単振動の図。
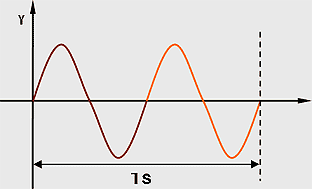
物理学において等速円運動あるいは単振動などの振動運動や波動が単位時間当たりに繰り返される回数。振動数は、運動の周期の逆数であり、単位はヘルツ(Hz)。
例えば、2Hzであれば、1秒間に2回の周期があるということ(下図参照)。
振動を発生させる機械および、仕組みのことを言う。主に電気による動電式振動発生機を指し、工業製品などの輸送試験や振動特性試験、振動を計測する加速度ピックアップを内蔵し、総じて品質試験を行う振動試験装置の構成する機械。
動電式振動発生機による振動は、サイン振動、ランダム振動、ショックがあり、計測された振動を再現する実波形などもある。
また、温度や湿度の負荷を加える温(湿)度試験槽(恒温恒湿槽)と組み合わせ環境試験装置を構成し、環境試験を行うこともできる。
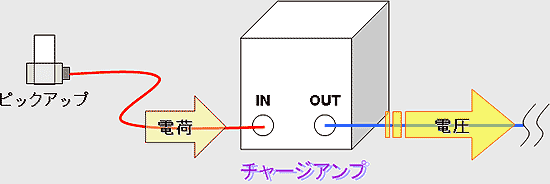
電荷信号を電圧信号に変換するためアンプ(増幅器)。
振動センサ(加速度ピックアップ)をはじめとする電荷型センサの計測では、計測器に電圧入力をするためチャージアンプを使用する。
電荷型計測器では、ピックアップ-チャージアンプ間に静電容量の変化が発生しノイズが含まれるため、専用ケーブルを使用する。
10倍の周波数比を持つ、2つの周波数の区間。
 で、求められる。
で、求められる。
系への入力と出力の数学的関係。
システムを構成する各要素で、信号がどのような形に変換され、伝達されていくかを示す伝達特性を示すもの。最も簡単な表現は出力と入力の比、「出力/入力」である。一般に入力、出力信号の比は時間関数で、入力信号が異なると変わり一定とはならない。そこで数学的には初期値をすべてゼロとした時の入力出力のラプラス変換の比にすれば、入力信号の大きさや波形に無関係となり一定を得る。

フレミングの左手の法則に従い、コイルに磁界を発生させ、加振力を生じさせる振動発生機。
動電式のメリットは、歪みのない波形が広帯域で再現できること、小型から大型まで作れること、設置が簡単であること、などが挙げられる。
与えられた時間の範囲内において、絶対値が最大となる箇所の値。
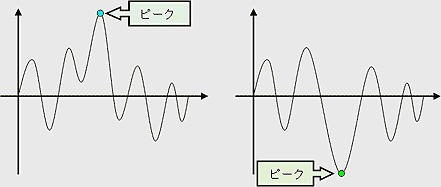
非周期的に時間関数を周波数成分に分解すること。一般的に実験などで得られた時間関数からフーリエ係数を求める場合、その関数が周期的に、無限に繰り返されているものと仮定して計算する。
(実際に計算する場合、積分範囲は有限である)
逆に周波数成分に分解された関数を、時間関数に変換することを逆フーリエ変換と言う。
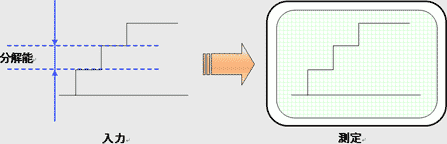
分解能とは、読み取る事が出来る測定値の最小変化。 すなわち、測定方式または測定機器によって決定される測定の細かさの限界(識別限界)。センサや計測装置が読み取れる最小単位や、解像度などが該当する。一般的に分解能が高ければ精度が高い。
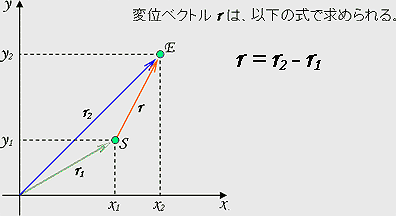
ある物が、ある位置からどれだけ動いたかを表す量。
物理(力学)的に、変位は位置の変化を表すベクトルであり、開始点(S点)と終了点(E点)の位置ベクトルの差である。振動数が低いほど、大きな変位で加振できる。
応答に再現性がなく、系の応答を確定量として予知できないとき、これをランダム(不規則振動)と呼ぶ。ランダム波形はフーリエ分析するとサイン波の集合体で、位相、振幅が変化したサイン波形を重ね合わせると、ランダム波振動になる。そのためランダム振動を加えると同時に多くの振動数成分で振動させることができるため、共振現象の特性試験などの、振動試験が短時間で実施できる。
不規則振動論では、確率論や確率過程論の手法を振動理論と組み合わせて、確率論的立場から構造や系の応答計算ならびに信頼性解析、安全性評価を行う。
おもなランダムの信頼性試験としてISO規格、IEC規格、ASTM規格、JIS規格、MIL規格など、公的な振動試験規格が用意されている。